The Midpoint Calculator simplifies finding the center point between two coordinates, making geometry tasks easier for students and professionals. It provides quick, accurate results without manual calculations, useful for problems involving line segments, symmetry, or locating centers. This tool saves time and reduces errors in geometric work. We’ll explore how the Midpoint Calculator works and how it can enhance your problem-solving in geometry, whether you’re tackling homework or handling precise measurements in professional projects.
What is a Midpoint?
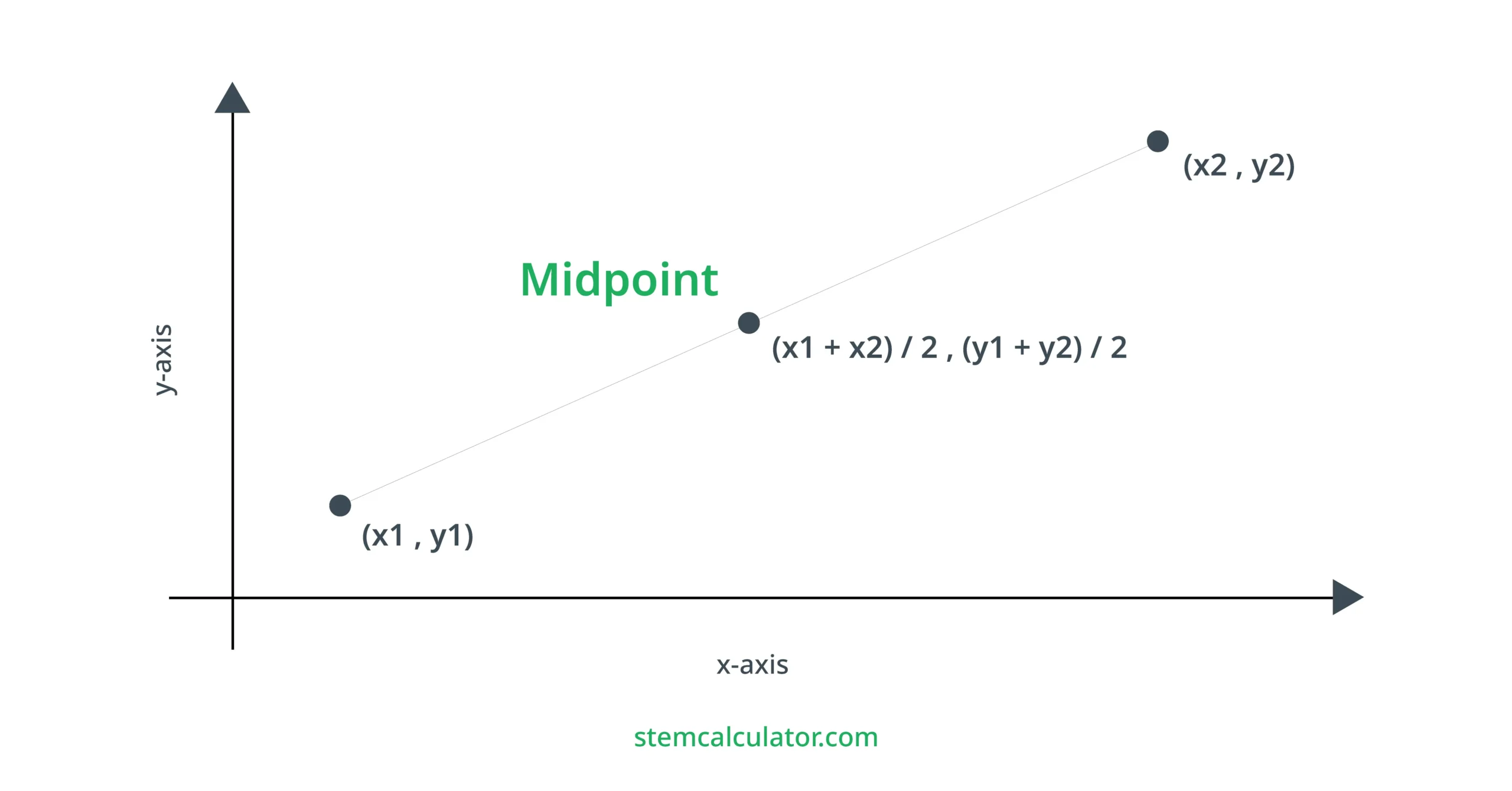
A midpoint is exactly what it sounds like – the middle point of a line segment. It’s a key concept in geometry, providing a balance point that divides a segment into two equal parts. Think of it as the fulcrum of a seesaw, where both sides are perfectly balanced. Knowing how to find the midpoint is crucial in various fields, from engineering to computer graphics.
The Midpoint Formula
The midpoint formula is your gateway to precision in geometry. It’s elegantly simple yet profoundly useful:
Midpoint M = (x1+x2 / 2 , y1+y2 / 2)
where, (x1,y1) and (x2,y2) are the coordinates of the two endpoints.
This formula averages the x-coordinates and the y-coordinates of the endpoints to find the midpoint. It’s a straightforward calculation that yields the exact center point between two locations.
| Endpoint 1 (x1, y1) | Endpoint 2 (x2, y2) | Midpoint (M) |
| (2, 3) | (10, 7) | (6, 5) |
| (1, 4) | (5, 8) | (3, 6) |
| (-3, -2) | (7, 4) | (2, 1) |
How to Use the Midpoint Calculator
Using the Midpoint Calculator on our website is a breeze. Here’s a step-by-step guide:
- Enter the Coordinates: Input the coordinates of the two endpoints. For example, if your endpoints are A(2,3) and B(10,7), enter these values into the calculator.
- Calculate: Hit the calculate button, and let the tool do the math for you.
- View Results: Instantly, the calculator will display the midpoint coordinates. In our example, the midpoint MMM would be (2+10 / 2, 3+7 / 2)=(6,5).
Not only does this save time, but it also ensures accuracy, especially useful when dealing with complex data or multiple calculations.
Practical Applications
The Midpoint Calculator is not just for academic exercises. It has practical applications across various fields:
- Architecture and Engineering: For precise measurements and structural balance, architects use the midpoint to find the center of structural elements, ensuring stability and symmetry in design. Engineers might use midpoints to calculate the center of gravity or to balance loads effectively. The midpoint formula is essential for accurate design and construction, helping professionals ensure that their structures are well-balanced and stable.
- Computer Graphics: To find the center point for graphical transformations and rendering, midpoints are crucial. In digital imaging, midpoints help in cropping, rotating, and scaling images accurately. By finding the midpoint, graphic designers can create balanced and aesthetically pleasing designs. Understanding how to find the midpoint of a line segment or between two points can significantly enhance the precision of graphical work.
- Navigation and GPS: Midpoint calculations are vital in determining the exact middle point between two geographical locations. This is particularly useful in planning routes, meeting points, and understanding geographical data. Midpoint calculations can help in logistics and transportation by optimizing paths and reducing travel time. For instance, if you need to find the midpoint between two coordinates on a map, using the midpoint formula can provide an accurate location.
- Construction: In construction projects, midpoints help in laying foundations, dividing plots, and ensuring structures are built correctly. For example, when installing a beam between two supports, knowing the midpoint can help in placing it accurately. This ensures the stability and structural integrity of the construction. Calculating the midpoint of a line segment, whether on a blueprint or in real-world applications, is crucial for accurate plotting and planning. The practical implications of these calculations in construction are detailed in various industry standards and guidelines.